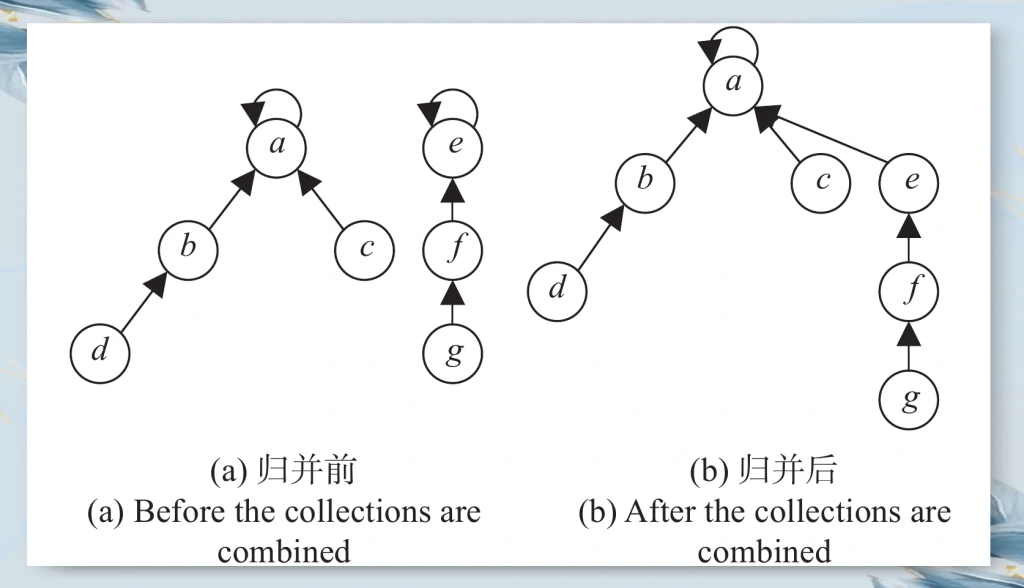
可持久化线段树(Persistent Segment Tree),又称主席树,是一种支持查询历史版本的数据结构。它在普通线段树的基础上通过共用节点来存储多个版本,从而高效地维护历史信息。
核心原理
1. 基本概念
可持久化线段树的核心思想是:每次修改只创建被修改路径上的新节点,其余节点与旧版本共享。这样既保留了历史版本,又避免了完全复制整棵树的空间浪费。
2. 关键特性
- 版本控制:每个版本对应一个根节点,通过根节点可以访问该版本的完整线段树
- 路径复制:修改操作只复制从根到目标节点的路径,空间复杂度O(log n)
- 前缀和思想:常用于解决区间第k大问题,通过版本相减得到区间信息
3. 数学基础
对于n次操作,可持久化线段树的空间复杂度为O(n logn),每次操作的时间复杂度为O(log n)。
C++实现
1. 基础结构
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10; // 数据规模
const int M = N * 20; // 节点数量估计
struct Node {
int l, r; // 左右子节点指针
int sum; // 区间和/计数
} tr[M];
int root[N], idx; // 各版本根节点和节点计数器
vector<int> nums; // 离散化数组
2. 离散化处理
// 离散化预处理
void discretize(vector<int>& a) {
nums = a;
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
}
// 获取离散化后的值
int get_id(int x) {
return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}
3. 建树与更新
// 建立初始空树
int build(int l, int r) {
int p = ++idx;
if (l == r) return p;
int mid = (l + r) >> 1;
tr[p].l = build(l, mid);
tr[p].r = build(mid + 1, r);
return p;
}
// 更新操作(创建新版本)
int update(int p, int l, int r, int x) {
int q = ++idx;
tr[q] = tr[p]; // 复制原节点
if (l == r) {
tr[q].sum++;
return q;
}
int mid = (l + r) >> 1;
if (x <= mid) tr[q].l = update(tr[p].l, l, mid, x);
else tr[q].r = update(tr[p].r, mid + 1, r, x);
tr[q].sum = tr[tr[q].l].sum + tr[tr[q].r].sum;
return q;
}
4. 查询操作
// 查询区间[l,r]的第k小值
int query(int p, int q, int l, int r, int k) {
if (l == r) return l;
int mid = (l + r) >> 1;
int cnt = tr[tr[q].l].sum - tr[tr[p].l].sum; // 左子树的元素个数
if (k <= cnt) return query(tr[p].l, tr[q].l, l, mid, k);
else return query(tr[p].r, tr[q].r, mid + 1, r, k - cnt);
}
5. 使用示例(区间第k小)
int main() {
int n, m;
scanf("%d%d", &n, &m);
vector<int> a(n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
discretize(a);
root[0] = build(1, nums.size());
for (int i = 1; i <= n; i++)
root[i] = update(root[i-1], 1, nums.size(), get_id(a[i-1]));
while (m--) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
int pos = query(root[l-1], root[r], 1, nums.size(), k);
printf("%d\n", nums[pos-1]);
}
return 0;
}
应用场景
- 区间第k大/小问题:通过版本相减得到区间统计信息
- 可持久化数组:支持历史版本的单点查询和修改
- 二维数点问题:结合扫描线使用
- 带修改的区间查询:结合树状数组实现
性能优化
- 动态开点:避免预分配大数组,按需创建节点
- 内存池:预先分配节点内存,减少动态分配开销
- 垃圾回收:对于不再使用的版本,可以回收节点空间