深入解析哈希表冲突解决方法：原理、实现与优化

哈希表是计算机科学中最重要、应用最广泛的数据结构之一，它能够在平均O(1)时间复杂度内完成数据的插入、删除和查找操作。然而，哈希表的高效性依赖于如何妥善解决哈希冲突——即不同键映射到同一位置的问题。

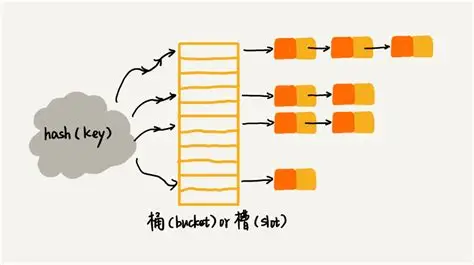
一、哈希冲突的本质与影响

哈希冲突是指两个或多个不同的键通过哈希函数计算后得到相同的哈希值或映射到同一存储位置的现象。这种现象几乎无法避免，因为哈希函数通常需要将大范围的键（甚至是无限集合）映射到有限的存储空间中。

哈希冲突会带来两个主要问题：

查找效率下降：冲突导致需要额外的处理步骤才能找到正确的元素
空间利用率降低：某些位置可能过度拥挤而其他位置空闲

影响冲突概率的关键因素：

哈希函数的质量：好的哈希函数应使输出均匀分布
装载因子(α)：元素数量/哈希表大小，通常α>0.7时冲突概率显著增加
哈希表大小：素数大小的表通常能更好地分散键

二、开放定址法家族

开放定址法的核心思想是：当目标位置已被占用时，按照某种探测序列寻找下一个可用位置。所有元素都存储在哈希表本身中，不需要额外的存储结构。

1. 线性探测法

原理：
当h(key)位置被占用时，顺序检查h(key)+1, h(key)+2,…直到找到空位。

实现示例：

def linear_probing_insert(table, key, value):
    index = hash(key) % len(table)
    while table[index] is not None and table[index][0] != key:
        index = (index + 1) % len(table)  # 环形查找
    table[index] = (key, value)

特点：

✅ 优点：
- 实现极其简单
- 缓存友好（连续内存访问）
❌ 缺点：
- 容易产生”一次聚集”（Primary Clustering）现象，即已占用的位置形成连续块，导致后续插入需要更长的探测路径
- 平均查找时间随着装载因子增加而急剧上升

优化变种：

线性探测+懒惰删除：标记删除位置而非直接置空，避免查找链断裂
线性探测+移动插入：插入时如果遇到已删除位置，可以移动后续元素填充

2. 平方探测法

原理：
探测序列改为使用平方增量：h(key)+1², h(key)+2², h(key)+3²,…

数学表达：
h(key, i) = (h(key) + c₁i + c₂i²) mod m
其中c₂≠0保证平方性质

实现示例：

def quadratic_probing_insert(table, key, value):
    index = hash(key) % len(table)
    i = 1
    while table[index] is not None and table[index][0] != key:
        index = (index + i*i) % len(table)  # 平方增量
        i += 1
    table[index] = (key, value)

特点：

✅ 优点：
- 减轻了一次聚集问题
- 比线性探测分布更均匀
❌ 缺点：
- 可能出现”二次聚集”（Secondary Clustering）——不同键使用相同的探测序列
- 不保证一定能找到空位（即使表未满）
- 缓存局部性不如线性探测

数学保证：
当表大小m为素数且装载因子α<0.5时，平方探测一定能找到空位。

3. 双重哈希法

原理：
使用第二个哈希函数计算探测步长：h(key, i) = (h₁(key) + i*h₂(key)) mod m

实现示例：

def double_hash_insert(table, key, value):
    h1 = hash1(key) % len(table)
    h2 = hash2(key) % (len(table)-1) + 1  # 确保与m互质
    i = 0
    index = (h1 + i*h2) % len(table)
    while table[index] is not None and table[index][0] != key:
        i += 1
        index = (h1 + i*h2) % len(table)
    table[index] = (key, value)

特点：

✅ 优点：
- 最均匀的开放定址方法
- 几乎消除了聚集现象
- 对于高装载因子表现良好
❌ 缺点：
- 需要计算两个哈希函数
- 缓存不友好（访问模式随机）
- h₂(key)必须与表大小m互质以确保探测序列覆盖全表

设计要点：

h₂(key)的结果应≠0
通常使m为素数，并令h₂(key)∈[1, m-1]

三、链地址法

链地址法采用完全不同的思路——允许每个位置存储多个元素，通常通过链表实现。

基本实现

数据结构：
哈希表的每个槽位都是一个链表头指针，冲突元素追加到链表末尾。

Java风格实现示例：

class HashMap<K,V> {
    private Node<K,V>[] table;
    
    static class Node<K,V> {
        final K key;
        V value;
        Node<K,V> next;
        // 构造方法...
    }
    
    public void put(K key, V value) {
        int index = hash(key) % table.length;
        for (Node<K,V> node = table[index]; node != null; node = node.next) {
            if (node.key.equals(key)) {
                node.value = value; // 更新
                return;
            }
        }
        // 插入新节点到链表头部
        table[index] = new Node<>(key, value, table[index]);
    }
}

优化演进

链表转红黑树（Java HashMap）：
- 当链表长度超过阈值（如8），转为红黑树
- 当节点数减少到阈值以下（如6），转回链表
- 平衡了极端情况下的性能
动态扩容：
- 当元素数量超过容量×装载因子时扩容
- 通常扩容为2倍，保持长度为2的幂
缓存优化：
- 某些实现（如Go）使用连续存储的键值对数组+溢出指针
- 每个桶可以存储多个键值对（如8个），减少指针追踪

性能分析

时间复杂度：

最优：O(1)（无冲突）
最坏：O(k)（所有键冲突，k为元素数量）
平均：O(1+α)（α为装载因子）

空间开销：

每个元素需要额外的指针空间
指针在64位系统占用8字节

与开放定址法对比：

维度	链地址法	开放定址法
高装载因子	性能下降平缓	性能急剧下降
内存使用	额外指针开销	无额外开销
删除操作	简单	需要特殊标记
缓存友好度	较差（节点分散）	较好（数据连续）
实现复杂度	较简单	需要考虑聚集问题

四、进阶方法与应用场景

1. 布谷鸟哈希（Cuckoo Hashing）

核心思想：
使用两个哈希表和两个哈希函数，每个键在两个表中只有一个可能位置。插入时如果两个位置都被占，则”踢出”其中一个现有元素。

算法步骤：

计算key的两个位置：h₁(key)和h₂(key)
如果任一位置为空，插入
否则，随机踢出一个位置的现有元素，插入新元素
对被踢出的元素，用另一个哈希函数重新计算位置并尝试插入
重复上述过程直到所有元素都找到位置或达到最大迭代次数（此时需要扩容或重建）

特点：

✅ 优点：
- 最坏情况查找时间为O(1)
- 高空间利用率（可达95%）
❌ 缺点：
- 插入成本可能很高（需要多次重定位）
- 需要维护两个哈希表

应用场景：

需要严格查找时间保证的系统
静态或较少变化的数据集

2. 罗宾汉哈希（Robin Hood Hashing）

核心思想：
在开放定址法中，让”更富有的”（即探测次数少的）元素让位于”更贫穷的”（探测次数多的）元素，减少最大探测距离。

实现要点：

每个元素记录其探测次数（PSL）
插入时如果遇到PSL更小的元素，交换位置并继续插入
查找时按照原始哈希顺序进行

特点：

✅ 优点：
- 显著降低最大探测距离
- 查找性能更稳定
❌ 缺点：
- 实现复杂
- 删除操作麻烦

3. 跳房子哈希（Hopscotch Hashing）

核心思想：
结合开放定址法和链地址法的优点，每个位置周围定义一个邻域（如32个位置），冲突元素放在邻域内。

特点：

通过位图记录邻域占用情况
查找只需检查邻域位置
结合了开放定址法的缓存优势和链地址法的冲突处理能力

五、工业级实现案例分析

1. Go语言map实现

核心特点：

链地址法的变种：每个桶存储8个键值对
使用溢出桶处理额外冲突
渐进式扩容：在写入时分批迁移数据

内存布局：

hmap
│
├── buckets → [bmap0, bmap1, ..., bmap2^B-1]
│               │
│               ├── tophash [8]uint8
│               ├── keys    [8]keytype
│               ├── values  [8]valuetype
│               └── overflow *bmap
└── oldbuckets → 旧桶数组（扩容时使用）

扩容策略：

装载因子>6.5或溢出桶过多时触发
每次迁移1-2个桶，分摊成本

2. Java HashMap

演进历史：

JDK1.7：纯链表解决冲突
JDK1.8+：链表长度>8转为红黑树

关键参数：

默认容量：16
装载因子：0.75
树化阈值：8
解树化阈值：6

并发问题：

非线程安全，多线程操作可能导致循环链表
ConcurrentHashMap采用分段锁保证线程安全

六、如何选择合适的冲突解决方法

选择冲突解决策略时应考虑以下因素：

数据特征：
- 键的分布：是否容易产生冲突
- 数据量大小：小数据集开放定址法可能更优
- 静态vs动态：静态数据可以考虑完美哈希
性能需求：
- 查找密集型：链地址法或布谷鸟哈希
- 插入密集型：考虑罗宾汉哈希或跳房子哈希
- 内存敏感：开放定址法
硬件特性：
- 缓存敏感：开放定址法通常更好
- 指针成本高：避免链地址法
并发需求：
- 高并发：考虑分段锁或读写锁
- 单线程：简单方法即可

通用建议：

通用场景：链地址法（Java风格）或高质量开放定址法
高性能需求：考虑布谷鸟哈希或罗宾汉哈希
内存受限：开放定址法
并发环境：java.util.concurrent.ConcurrentHashMap风格的分段锁

深入解析哈希表冲突解决方法：原理、实现与优化

一、哈希冲突的本质与影响

二、开放定址法家族

1. 线性探测法

2. 平方探测法

3. 双重哈希法

三、链地址法

基本实现

优化演进

性能分析

四、进阶方法与应用场景

1. 布谷鸟哈希（Cuckoo Hashing）

2. 罗宾汉哈希（Robin Hood Hashing）

3. 跳房子哈希（Hopscotch Hashing）

五、工业级实现案例分析

1. Go语言map实现

2. Java HashMap

六、如何选择合适的冲突解决方法

相关文章