ST表 (Sparse Table )

定义

ST 表（Sparse Table，稀疏表）是用于解决 可重复贡献问题 的数据结构。

可重复贡献问题 是指对于运算 opt，满足 x opt x = x，则对应的区间询问就是一个可重复贡献问题。例如，最大值有 max(x,x) = x ，gcd 有 gcd(x,x) = x ，所以 RMQ（区间最值查询） 和区间 GCD（最大公约数） 就是一个可重复贡献问题。像区间和就不具有这个性质，如果求区间和的时候采用的预处理区间重叠了，则会导致重叠部分被计算两次，这是我们所不愿意看到的。另外，opt 还必须满足结合律才能使用 ST 表求解。

引入

ST 表模板题

题目大意：给定 N 个数，有 M个询问，对于每个询问 L,R ，你需要回答区间 [L,R]中的最大值。

考虑暴力做法。每次都对区间[L,R]扫描一遍，求出最大值。

显然，这个算法会超时。

ST 表

ST 表基于倍增思想，可以做到 O(N * log ^N)预处理，O(1) 回答每个询问。但是不支持修改操作。

基于倍增思想，我们考虑如何求出区间最大值。可以发现，如果按照一般的倍增流程，每次跳 2ⁱ 步的话，询问时的复杂度仍旧是 O(log^N) ，并没有比线段树更优，反而预处理一步还比线段树慢。

我们发现 max(x,x)=x ，也就是说，区间最大值是一个具有「可重复贡献」性质的问题。即使用来求解的预处理区间有重叠部分，只要这些区间的并是所求的区间，最终计算出的答案就是正确的。

如果手动模拟一下，可以发现我们能使用至多两个预处理过的区间来覆盖询问区间，也就是说询问时的时间复杂度可以被降至 O(1)，在处理有大量询问的题目时十分有效。

具体实现如下：

令 f(i,j) 表示区间 [i,i+2^j -1] 的最大值。

显然 f(i,0) = array[i]。

根据定义式，第二维就相当于倍增的时候「跳了  2^j -1步」，依据倍增的思路，写出状态转移方程：

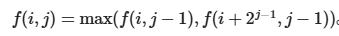
以上就是预处理部分。而对于查询，可以简单实现如下：

对于每个询问[l,r] ，把它分成两部分：

 其中 

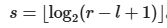
两部分的结果的最大值就是答案。

根据上面对于「可重复贡献问题」的论证，由于最大值是「可重复贡献问题」，重叠并不会对区间最大值产生影响。又因为这两个区间完全覆盖了 [l,r]，可以保证答案的正确性。

通过代码

#include <bits/stdc++.h>
using namespace std;

int st[112345][22];
int lg2[112345];

void initST(int n)
{
    for (int i = 2; i <= n; i++)
    {
        lg2[i] = lg2[i >> 1] + 1;
    }
    for (int j = 1; j <= lg2[n]; j++)
    {
        for (int i = 1; i + (1 << (j - 1)) <= n; i++)
        {
            st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
        }
    }
}

int RMQ(int l, int r)
{
    int s=lg2[r-l+1];
    return max(st[l][s], st[r - (1<<s)+1][s]);
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &st[i][0]);
    }
    initST(n);
    int l, r;
    while (m--)
    {
        scanf("%d%d", &l, &r);
        printf("%d\n", RMQ(l, r));
    }
    return 0;
}