树状数组（Fenwick Tree）

树状数组是一种高效维护前缀和的数据结构，支持单点更新和前缀查询操作，时间复杂度均为 O(logn)。其核心思想是通过二进制分解将前缀和拆分为若干子数组的和。

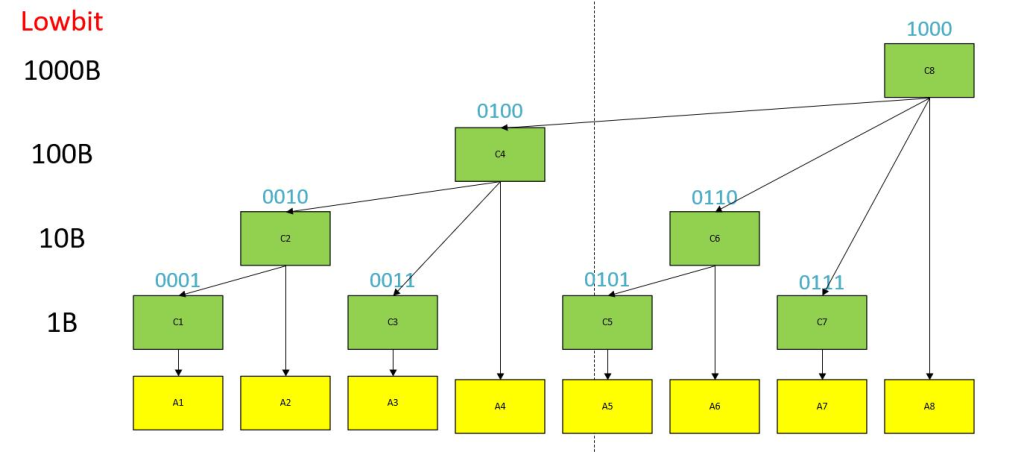
​​核心思想​​

1. 二进制索引：
   • 每个整数 i 可以表示为二进制形式（如 6=1102​）。 • 定义 lowbit(i) 为 i 的二进制表示中最低位的 1 所对应的值（如 lowbit(6) = 2）。 • lowbit(i) 的计算方式：i & -i（利用补码性质）。
2. 树状结构：
   • 数组 tree 中，tree[i] 存储的是原数组 a 中区间 [i - lowbit(i) + 1, i] 的和。 • 通过 lowbit 跳跃式访问，将前缀和分解为 O(logn) 个 tree 节点的和。

​​操作实现​​

1. 单点更新（update）：
   • 修改 a[x] 后，需要更新所有包含 a[x] 的 tree 节点。 • 从 x 开始，每次向上跳 lowbit(x)，直到超出数组范围。
2. 前缀查询（query）：
   • 查询前缀和 sum[1..x] 时，从 x 开始，每次累加 tree[x]，然后向上跳 x -= lowbit(x)，直到 x = 0。

​​正确性证明​​

1. 更新覆盖性：
   • 每次更新 x 时，x + lowbit(x) 会跳到下一个覆盖 a[x] 的父节点。例如： ◦ 更新 x=1（lowbit(1)=1）会影响 1, 2, 4, 8,...。 ◦ 更新 x=6（lowbit(6)=2）会影响 6, 8,...。 • 通过二进制位的进位，确保所有相关区间被更新。
2. 查询完整性：
   • 前缀和 sum[1..x] 被分解为 tree[x] + tree[x - lowbit(x)] + ...。 • 每次 x -= lowbit(x) 会跳到下一个不重叠的区间，确保所有子区间被累加。

​​时间复杂度证明​​
• 单点更新：每次跳跃 lowbit(x)，相当于在二进制表示中从右向左移动 1 的位置，最多 O(logn) 次。

• 前缀查询：同理，每次跳跃 lowbit(x)，最多 O(logn) 次。

• 初始化：通过 n 次更新操作构建，复杂度 O(nlogn)。

​​C++ 实现​

​

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 5e5 + 5;
int a[MAXN], c[MAXN];
int n, m;
int lowbit(int x)
{
    return x & -x;
}

void update(int pos, int value)
{
    while (pos <= n)
    {
        c[pos] += value;
        pos += lowbit(pos);
    }
}

int getPreSum(int right)
{
    int sum = 0;
    while (right > 0)
    {
        sum += c[right];
        right -= lowbit(right);
    }
    return sum;
}

int getRangeSum(int left, int right)
{
    return getPreSum(right) - getPreSum(left - 1);
}

int main()
{

    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        update(i, a[i]);
    }

    int op, l, r;
    while (m--)
    {
        scanf("%d%d%d", &op, &l, &r);
        switch (op)
        {
        case 1:
            update(l, r);
            break;
        case 2:
            printf("%d\n", getRangeSum(l, r));
            break;
        default:
            break;
        }
    }
    return 0;
}

​

​​应用场景​​
• 动态维护前缀和（如频繁更新的数组）。

• 逆序对计数（离散化后插入统计）。

• 替代线段树（当仅需前缀操作时更高效）。

树状数组通过巧妙的二进制设计，以极低的代码复杂度实现了高效的前缀操作。